一、基础知识形如ax+by=c(a，b，c∈Z，且ab≠0)
(1-1)
的不定方程称为二元一次不定方程.
下面给出二元一次不定方程整数解的存在性的相关定理.
定理1.1[1] (1-1)式有整数解的充分与必要条件是(a，b)|c.
定理1.2[1] 设二元一次不定方程ax+by=c(其中a，b，c是整数，且ab≠0)有一整数解x=x0，y=y0；又设(a，b)=d，a=a1d，b=b1d，则(1-1)的一切解可以表示成
x=x0-b1t，y=y0+a1t(t=0，±1，±2，…).
(1-2)
二、解题方法(一)观察法观察法适用于a|c或b|c的情况.若a|c，则令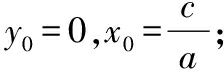
若b|c，则令
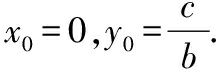由x0，y0及定理1.2可表示出不定方程的所有整数解.
例1 中国古代数学家张丘建曾经解答了下面的题目：
“鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一.百钱买百鸡.问鸡翁、母、雏各几何？”
设用x，y，z分别代表鸡翁、鸡母、鸡雏的数目，可得到如下不定方程组：
消去z即得二元一次不定方程7x+4y=100.
解 因为(7，4)=1，得(7，4)|100，所以由定理1.1知原方程有整数解.
又因为4|100，所以可得到方程的一组特解x0=0，y0=25，并且a1=7/(7，4)，b1=4/(7，4)，由定理1.2知原方程的一切整数解可以表示为
x=-4t，y=25+7t，t=(0，±1，±2，…).
(2-1)
因为x≥0，y≥0，所以易得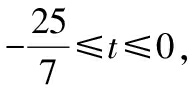
即t=-3，-2，-1，0.将t=-3，-2，-1，0分别代入(2-1)式，求出x，y的值，再将x，y的值代入等式z=100-x-y，得z的值.这样就得到了以下四组结果：
只有当不定方程的特解很容易求得时，这个方法才很适用.
(二)同余法同余法[2-4]就是利用同余理论解决不定方程问题的方法.
通常，我们研究不定方程
f(x1，…，xn)=0
(2-2)
的整数解，这里f(x1，…，xn)是n元整系数多项式.(2-2)对应的同余式为
f(x1，…，xn)≡0(modm).
(2-3)
这里m>1，是给定的整数.
定理2.1[5] 不定方程(2-2)有整数解，则同余式(2-3)对所有的正整数m>1有解.
例2 用解同余式法求例1中不定方程的非负整数解.
解 取模4可得原方程等价于同余式7x≡3x≡0(mod4)，此同余式的解为x≡0(mod4)，即x=-4t(t=0，±1，±2，…)，把x=-4t代入原方程得y=25+7t(t=0，±1，±2，…).
由题意可知x≥0，y≥0，因此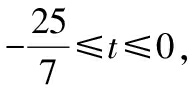
故t=-3，-2，-1，0.
又鸡雏数是z=100-x-y=-3t，
这样就得到了以下四组结果：
用同余法求解不定方程可以避免复杂的求特解过程.
【参考文献】
[1]Schmidt W M Diophantine Approximation and Diophantine Equations[M].Berlin：Springer-Verlag，1991.
[2]乐茂华.Gelfond-Baker方法在丢番图方程中的应用[M].北京：科学出版社，1998.
[3]柯召，孙琦.数论讲义(下册)：第2版[M].北京：高等教育出版社，2003.
[4]Burn R P.A Pathway into Number Theory[M].Cambridge:Cambridge University Press,1982.
[5]曹珍富.不定方程及应用[M].上海：上海交通大学出版社，2000.
